Réseaux neuronaux convolutifs

Les réseaux de neurones convolutifs (aussi appelés ConvNets) sont conçus pour tirer parti de la structure des données. Dans ce chapitre, nous aborderons deux types de réseaux convolutifs : nous commencerons par le cas monodimensionnel et verrons comment les réseaux convolutifs à convolutions 1D peuvent être utiles pour traiter les séries temporelles. Nous présenterons ensuite le cas 2D, particulièrement utile pour traiter les données d’image.

Réseaux de neurones convolutifs pour les séries temporelles

Les réseaux de neurones convolutifs pour les séries temporelles reposent sur l’opérateur de convolution 1D qui, étant donné une série temporelle \(\mathbf{x}\) et un filtre \(\mathbf{f}\), calcule une carte d’activation comme :

(2)\[\begin{equation} \left(\mathbf{x} * \mathbf{f}\right)(t) = \sum_{k=-L}^L f_{k} x_{t + k} \label{eq:conv1d} \end{equation}\]

où le filtre \(\mathbf{f}\) est de longueur \((2L + 1)\).

Le code suivant illustre cette notion en utilisant un filtre gaussien :

Show code cell content

Hide code cell content

%config InlineBackend.figure_format = 'svg'
%matplotlib inline
import matplotlib.pyplot as plt
from notebook_utils import prepare_notebook_graphics
prepare_notebook_graphics()

import numpy as np

def random_walk(size):
    rnd = np.random.randn(size) * .1
    ts = rnd
    for t in range(1, size):
        ts[t] += ts[t - 1]
    return ts

np.random.seed(0)
x = random_walk(size=50)
f = np.exp(- np.linspace(-2, 2, num=5) ** 2 / 2)
f /= f.sum()

plt.figure()
plt.plot(x, label='Série temporelle')
plt.plot(np.correlate(x, f, mode='same'),
         label='Carte d\'activation (série temporelle passée à travers un filtre Gaussien)')
plt.legend();

Les réseaux de neurones convolutifs sont constitués de blocs de convolution dont les paramètres sont les coefficients des filtres qu’ils intègrent (les filtres ne sont donc pas fixés a priori comme dans l’exemple ci-dessus mais plutôt appris). Ces blocs de convolution sont équivariants par translation, ce qui signifie qu’un décalage (temporel) de leur entrée entraîne le même décalage temporel de leur sortie :

Show code cell source

Hide code cell source

from IPython.display import HTML
from celluloid import Camera

f = np.zeros((12, ))
f[:4] = -1.
f[4:8] = 1.
f[8:] = -1.

length = 60

fig = plt.figure()
camera = Camera(fig)

for pos in list(range(5, 35)) + list(range(35, 5, -1)):
    x = np.zeros((100, ))
    x[pos:pos+length] = np.sin(np.linspace(0, 2 * np.pi, num=length))

    act = np.correlate(x, f, mode='same')

    plt.subplot(2, 1, 1)
    plt.plot(x, 'b-')
    plt.title("Série temporelle")
    fig2 = plt.subplot(2, 1, 2)
    plt.plot(act, 'r-')
    plt.title("Carte d'activation")

    axes2 = fig.add_axes([.15, .35, 0.2, 0.1]) # renvoie un objet Axes
    axes2.plot(f, 'k-')
    axes2.set_xticks([])
    axes2.set_title("Filtre")

    plt.tight_layout()
    camera.snap()

anim = camera.animate()
plt.close()

HTML(anim.to_jshtml())

/tmp/ipykernel_6683/1028966743.py:32: UserWarning: This figure includes Axes that are not compatible with tight_layout, so results might be incorrect.
  plt.tight_layout()

Once Loop Reflect

Les modèles convolutifs sont connus pour être très performants dans les applications de vision par ordinateur, utilisant des quantités modérées de paramètres par rapport aux modèles entièrement connectés (bien sûr, des contre-exemples existent, et le terme « modéré » est particulièrement vague).

La plupart des architectures standard de séries temporelles qui reposent sur des blocs convolutionnels sont des adaptations directes de modèles de la communauté de la vision par ordinateur ([Le Guennec et al., 2016] s’appuie sur une alternance entre couches de convolution et couches de pooling, tandis que des travaux plus récents s’appuient sur des connexions résiduelles et des modules d”inception [Fawaz et al., 2020]). Ces blocs de base (convolution, pooling, couches résiduelles) sont discutés plus en détail dans la section suivante.

Ces modèles de classification des séries temporelles (et bien d’autres) sont présentés et évalués dans [Fawaz et al., 2019] que nous conseillons au lecteur intéressé.

Réseaux de neurones convolutifs pour les images

Nous allons maintenant nous intéresser au cas 2D, dans lequel les filtres de convolution ne glisseront pas sur un seul axe comme dans le cas des séries temporelles, mais plutôt sur les deux dimensions (largeur et hauteur) d’une image.

Images et convolutions

Comme on le voit ci-dessous, une image est une grille de pixels, et chaque pixel a une valeur d’intensité dans chacun des canaux de l’image. Les images couleur sont typiquement composées de 3 canaux (ici Rouge, Vert et Bleu).

Show code cell source

Hide code cell source

from matplotlib import image

image = image.imread('../data/cat.jpg')
image_r = image.copy()
image_g = image.copy()
image_b = image.copy()
image_r[:, :, 1:] = 0.
image_g[:, :, 0] = 0.
image_g[:, :, -1] = 0.
image_b[:, :, :-1] = 0.

plt.figure(figsize=(20, 8))
plt.subplot(2, 3, 2)
plt.imshow(image)
plt.title("Une image RGB")
plt.axis("off")

for i, (img, color) in enumerate(zip([image_r, image_g, image_b],
                                     ["Rouge", "Vert", "Bleu"])):
    plt.subplot(2, 3, i + 4)
    plt.imshow(img)
    plt.title(f"Canal {color}")
    plt.axis("off")

Fig. 2 Une image et ses 3 canaux (intensités de Rouge, Vert et Bleu, de gauche à droite).

La sortie d’une convolution sur une image \(\mathbf{x}\) est une nouvelle image, dont les valeurs des pixels peuvent être calculées comme suit :

(3)\[\begin{equation} \left(\mathbf{x} * \mathbf{f}\right)(i, j) = \sum_{k=-K}^K \sum_{l=-L}^L \sum_{c=1}^3 f_{k, l, c} x_{i + k, j + l, c} . \label{eq:conv2d} \end{equation}\]

En d’autres termes, les pixels de l’image de sortie sont calculés comme le produit scalaire entre un filtre de convolution (qui est un tenseur de forme \((2K + 1, 2L + 1, c)\)) et un patch d’image centré à la position donnée.

Considérons, par exemple, le filtre de convolution 9x9 suivant :

Show code cell source

Hide code cell source

sz = 9

filter = np.exp(-(((np.arange(sz) - (sz - 1) // 2) ** 2).reshape((-1, 1)) + ((np.arange(sz) - (sz - 1) // 2) ** 2).reshape((1, -1))) / 100.)
filter_3d = np.zeros((sz, sz, 3))
filter_3d[:] = filter.reshape((sz, sz, 1))


plt.figure()
plt.imshow(filter_3d)
plt.axis("off");

Le résultat de la convolution de l’image de chat ci-dessus avec ce filtre est l’image suivante en niveaux de gris (c’est-à-dire constituée d’un seul canal) :

Show code cell source

Hide code cell source

from scipy.signal import convolve2d

convoluted_signal = np.zeros(image.shape[:-1])
for c in range(3):
    convoluted_signal += convolve2d(image[:, :, c], filter_3d[:, :, c], mode="same", boundary="symm")

plt.figure()
plt.imshow(convoluted_signal, cmap="gray")
plt.axis("off");

On peut remarquer que cette image est une version floue de l’image originale. C’est parce que nous avons utilisé un filtre Gaussien. Comme pour les séries temporelles, lors de l’utilisation d’opérations de convolution dans les réseaux neuronaux, le contenu des filtres sera appris, plutôt que défini a priori.

Réseaux convolutifs de type LeNet

Dans [LeCun et al., 1998], un empilement de couches de convolution, de pooling et de couches entièrement connectées est introduit pour une tâche de classification d’images, plus spécifiquement une application de reconnaissance de chiffres. Le réseau neuronal résultant, appelé LeNet, est représenté ci-dessous :

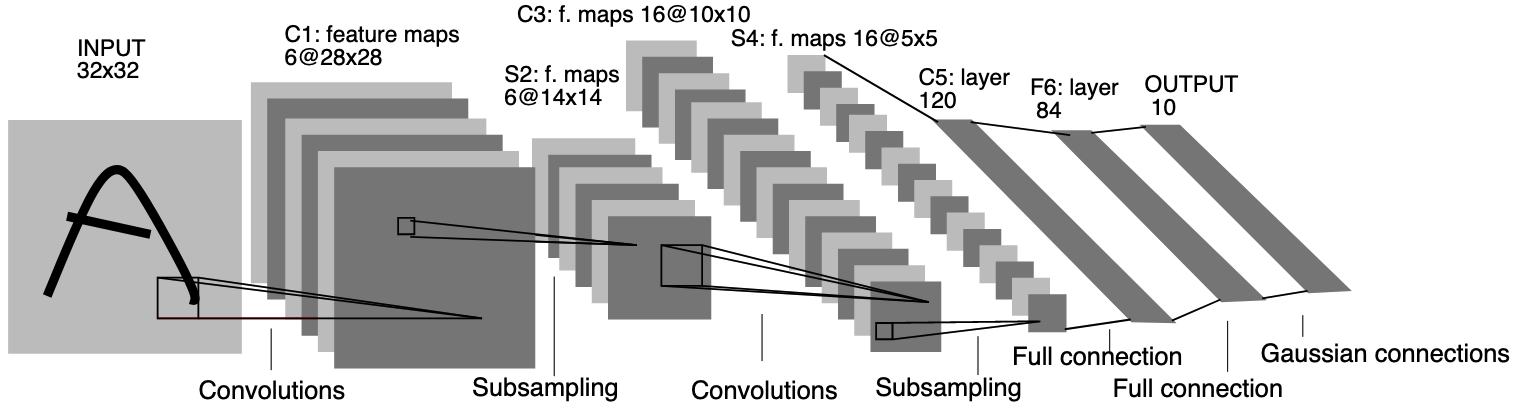
Fig. 3 Modèle LeNet-5

Couches de convolution

Une couche de convolution est constituée de plusieurs filtres de convolution (également appelés kernels) qui opèrent en parallèle sur la même image d’entrée. Chaque filtre de convolution génère une carte d’activation en sortie et toutes ces cartes sont empilées pour former la sortie de la couche de convolution. Tous les filtres d’une couche partagent la même largeur et la même hauteur. Un terme de biais et une fonction d’activation peuvent être utilisés dans les couches de convolution, comme dans d’autres couches de réseaux neuronaux. Dans l’ensemble, la sortie d’un filtre de convolution est calculée comme suit :

(4)\[\begin{equation} \left(\mathbf{x} * \mathbf{f}\right)(i, j, c) = \varphi \left( \sum_{k=-K}^K \sum_{l=-L}^L \sum_{c^\prime} f^c_{k, l, c^\prime} x_{i + k, j + l, c^\prime} + b_c \right) \label{eq:conv_layer} \end{equation}\]

où \(c\) désigne le canal de sortie (notez que chaque canal de sortie est associé à un filtre \(f^c\)), \(b_c\) est le terme de biais qui lui est associé et \(\varphi\) est la fonction d’activation utilisée.

Astuce

En keras, une telle couche est implémentée à l’aide de la classe Conv2D :

import keras
from keras.layers import Conv2D

layer = Conv2D(filters=6, kernel_size=5, padding="valid", activation="relu")

Padding

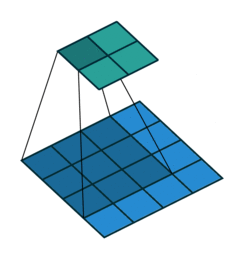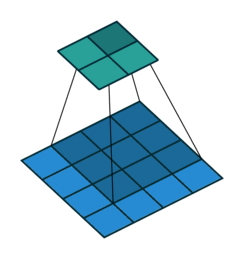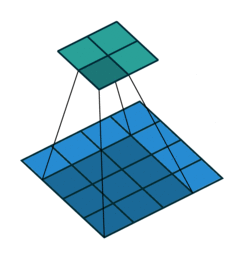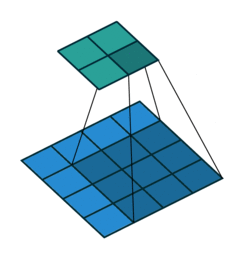
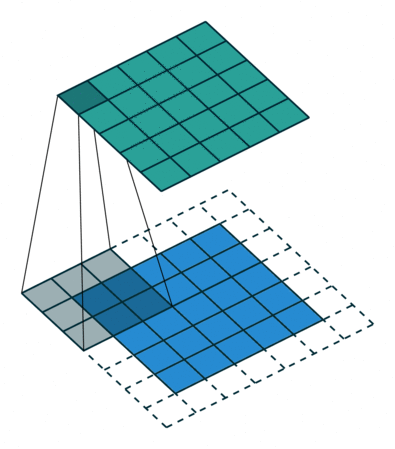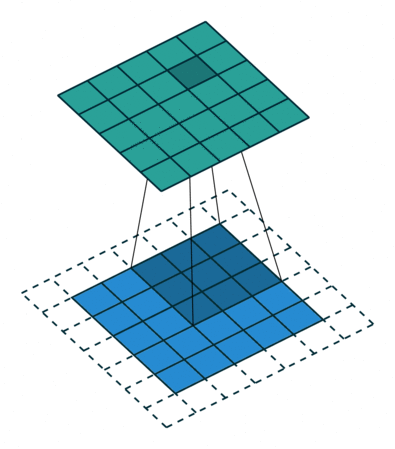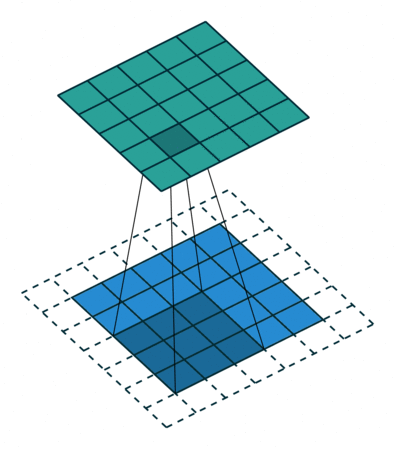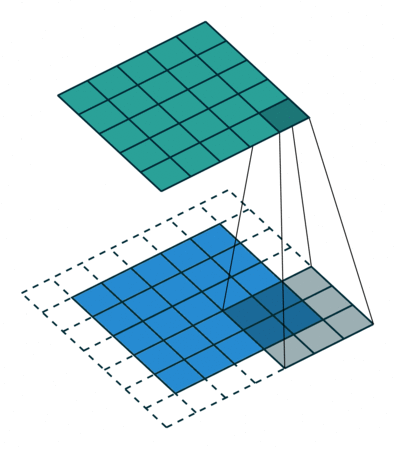
Fig. 4 Visualisation de l’effet du padding (source: V. Dumoulin, F. Visin - A guide to convolution arithmetic for deep learning). Gauche: sans padding, droite: avec padding.

Lors du traitement d’une image d’entrée, il peut être utile de s’assurer que la carte de caractéristiques (ou carte d’activation) de sortie a la même largeur et la même hauteur que l’image d’entrée. Cela peut être réalisé en agrandissant artificiellement l’image d’entrée et en remplissant les zones ajoutées avec des zéros, comme illustré dans Fig. 4 dans lequel la zone de padding est représentée en blanc.

Couches de pooling

Les couches de pooling effectuent une opération de sous-échantillonnage qui résume en quelque sorte les informations contenues dans les cartes de caractéristiques dans des cartes à plus faible résolution.

L’idée est de calculer, pour chaque parcelle d’image, une caractéristique de sortie qui calcule un agrégat des pixels de la parcelle. Les opérateurs d’agrégation typiques sont les opérateurs de moyenne (dans ce cas, la couche correspondante est appelée average pooling) ou de maximum (pour les couches de max pooling). Afin de réduire la résolution des cartes de sortie, ces agrégats sont généralement calculés sur des fenêtres glissantes qui ne se chevauchent pas, comme illustré ci-dessous, pour un max pooling avec une taille de pooling de 2x2 :

Ces couches étaient largement utilisées historiquement dans les premiers modèles convolutifs et le sont de moins en moins à mesure que la puissance de calcul disponible augmente.

Astuce

En keras, les couches de pooling sont implémentées à travers les classes MaxPool2D et AvgPool2D :

from keras.layers import MaxPool2D, AvgPool2D

max_pooling_layer = MaxPool2D(pool_size=2)
average_pooling_layer = AvgPool2D(pool_size=2)

Ajout d’une tête de classification

Un empilement de couches de convolution et de pooling produit une carte d’activation structurée (qui prend la forme d’une grille 2d avec une dimension supplémentaire pour les différents canaux). Lorsque l’on vise une tâche de classification d’images, l’objectif est de produire la classe la plus probable pour l’image d’entrée, ce qui est généralement réalisé par une tête de classification (classification head) composée de couches entièrement connectées.

Pour que la tête de classification soit capable de traiter une carte d’activation, les informations de cette carte doivent être transformées en un vecteur. Cette opération est appelée Flatten dans keras, et le modèle correspondant à Fig. 3 peut être implémenté comme :

from keras.models import Sequential
from keras.layers import InputLayer, Conv2D, MaxPool2D, Flatten, Dense

model = Sequential([
    InputLayer(input_shape=(32, 32, 1)),
    Conv2D(filters=6, kernel_size=5, padding="valid", activation="relu"),
    MaxPool2D(pool_size=2),
    Conv2D(filters=16, kernel_size=5, padding="valid", activation="relu"),
    MaxPool2D(pool_size=2),
    Flatten(),
    Dense(120, activation="relu"),
    Dense(84, activation="relu"),
    Dense(10, activation="softmax")
])
model.summary()

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ conv2d (Conv2D)                 │ (None, 28, 28, 6)      │           156 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d (MaxPooling2D)    │ (None, 14, 14, 6)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_1 (Conv2D)               │ (None, 10, 10, 16)     │         2,416 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_1 (MaxPooling2D)  │ (None, 5, 5, 16)       │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten (Flatten)               │ (None, 400)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 120)            │        48,120 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 84)             │        10,164 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_2 (Dense)                 │ (None, 10)             │           850 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 61,706 (241.04 KB)

 Trainable params: 61,706 (241.04 KB)

 Non-trainable params: 0 (0.00 B)

Références

[FFW+19]

Hassan Ismail Fawaz, Germain Forestier, Jonathan Weber, Lhassane Idoumghar, and Pierre-Alain Muller. Deep learning for time series classification: a review. Data Mining and Knowledge Discovery, 33(4):917–963, 2019.

[FLF+20]

Hassan Ismail Fawaz, Benjamin Lucas, Germain Forestier, Charlotte Pelletier, Daniel F Schmidt, Jonathan Weber, Geoffrey I Webb, Lhassane Idoumghar, Pierre-Alain Muller, and François Petitjean. Inceptiontime: finding alexnet for time series classification. Data Mining and Knowledge Discovery, 34(6):1936–1962, 2020.

[LGMT16]

Arthur Le Guennec, Simon Malinowski, and Romain Tavenard. Data Augmentation for Time Series Classification using Convolutional Neural Networks. In ECML/PKDD Workshop on Advanced Analytics and Learning on Temporal Data. Riva Del Garda, Italy, September 2016.

[LBBH98]

Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.